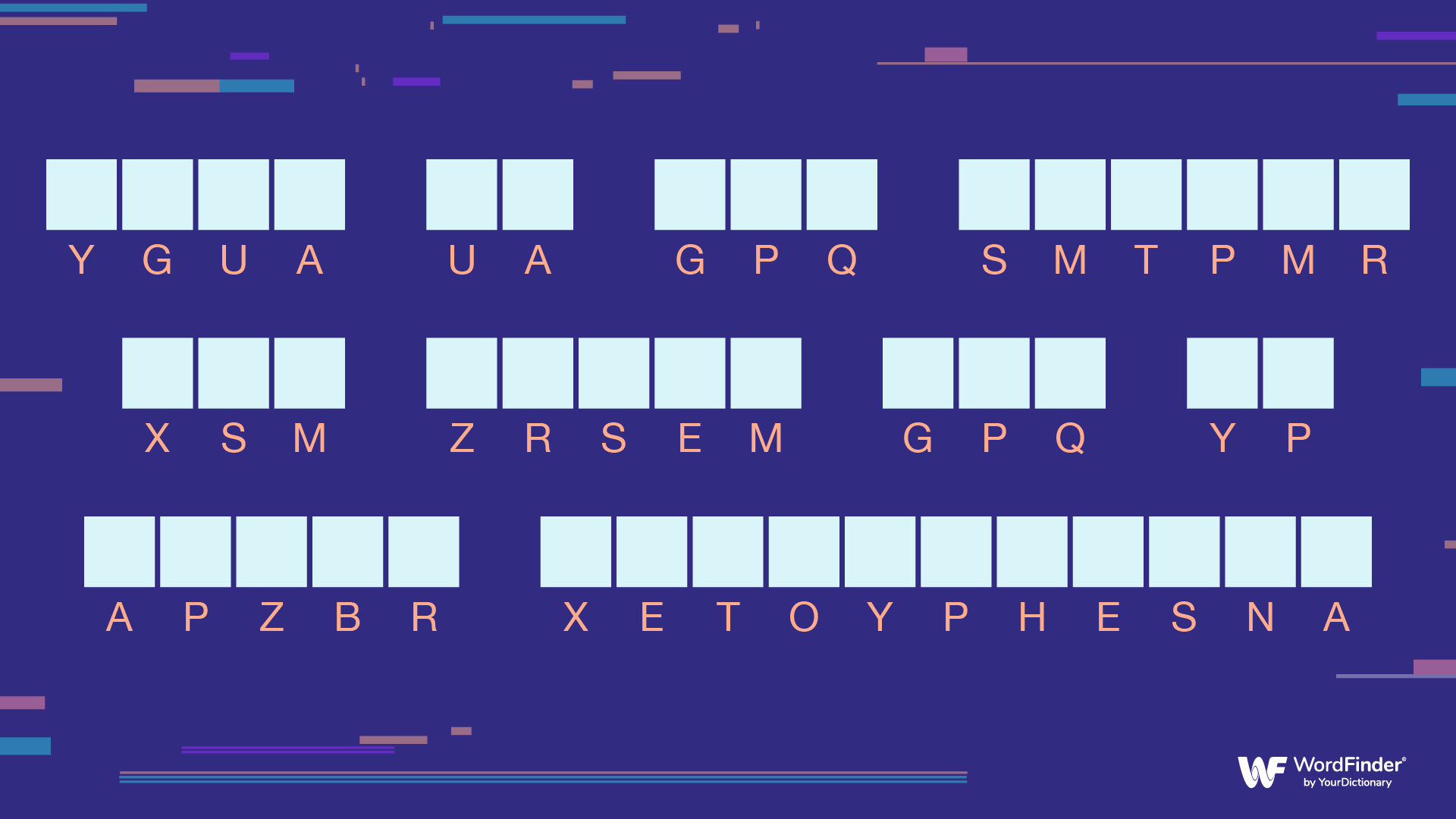
Most cryptograms are encoded with single-transposition keys, where one letter is substituted for another. This seems to create complete gibberish on a screen, such as:
Ygua ua gpq smtpmr xsm zrsem gpq yp apzbr xetoyphesna.
However, there are actually very clear and deliberate ways to figure out exactly which letters are substituted to find the meaning of the cryptogram.
The key, so to speak, is to look at some of the conventions of the English language and play a game of percentages and educated guesses.
Look for Popular Letters
The first step is to realize that the most common letters in the English language are E, T, A, O, and N, with I and S a close second.
So, to solve a cryptography puzzle, you should look at what letters occur most often in the gibberish word, and work with them.
Let's use the example from above: Ygua ua gpq smtpmr xsm zrsem gpq yp apzbr xetoyphesna.
M, R, and S appear three or four times each. Now, we can begin the process of trial and error by substituting the popular letters in this cryptogram for some more common ones.
Solve the Short Words
Solving for the short words can help you put a longer cryptogram sentence all together. This is especially effective for short words that have only two or three letters.
The most common two-letter words are:
of
to
in
is
it
as
he
be
by
on
or
at
For three letters, it gets a little more complicated. The most common three letter words are:
and
the
for
his
not
but
you
are
her
had
However, there are quite a few other three-letter words – for example (and to provide a hint to the solution) the three-letter words in the above cryptogram are actually can and how (one of them, GPQ, appears twice).
Spot the Repeated Letters
Other conventions of the English language can also provide clues. Only a few letters are actually ever repeated twice in a word: RR, LL, NN, MM, and fewer of these are in small words.
So, if there is a three-letter word containing repeating letters, such as SZZ, that word is almost certainly the word all.
Another very common pattern is the letters TH – they appear in both the and that, as well as this, those, them, and more.
Look for Digraphs
The technical term for two-letter combinations that commonly appear in the English language is digraphs.
The most common digraphs are:
TH
HE
AN
IN
ER
RE
ES
ON
EA
TI (this one is especially useful in discovering the common four-letter word ending –TION)
So, in the above cryptogram, the first word is this (spoiler alert). Now you know that the letter combination YG is actually TH. YG doesn't appear at the beginning of any other words, so you now know that none of them are words with TH at the beginning.
Go for the Unusual
Knowing what the words can't be is sometimes as useful as knowing what they can be. Also, knowing unusual words, such as those that begin with X, can give you a great advantage in solving cryptograms.
Don't Overlook the Obvious
Other conventions of cryptographic puzzles are also useful to know. Sometimes, cryptograms try to throw in non-transposed letters, so that all would be encoded GLL. The trick is that a person can spend forever trying to figure out what the letter L represents (the answer being itself).
Many cryptograms begin with phrases like "The best…", or "Some of the…", or "The only…", and knowing that can give you a few options to try right away.
Look for the Pattern
It all comes down to making systematic educated guesses until the pattern emerges. Usually, after the vowels are figured out, it is easy to finish solving the puzzle as the phrase becomes clear.
One frustrating problem can be a cryptogram with errors in it, whether grammatical, spelling, or an encoding error; however, that can be seen as just another bit of the puzzle to figure out, above and beyond the basic cryptographic algorithm.
So, What Is the Code?
Using these step-by-step processes, you can figure out that the puzzle at the beginning of the article uses the following substitution cipher:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
S V X F R D H G U K J Z N M P O W E A Y I B Q C T L
So the translated cryptogram reads: "This is how anyone can learn how to solve cryptograms."
Can't get enough word puzzles? Try your hand at anagrams or create your own word with our Word Maker tool.